第47回_同じ “Ｆ型” でも、縦横比率はまちまち…っていうハナシ

前回のメルマガに添付した “資料” が、意外なことに…ご好評でした 

『どこでダウンロード出来ますか？』とのお問い合わせもいただきましたが、あれはダウンロードなんか出来ません。

だってあれ、３ダースが自作した資料ですから… 

しかもパソコンじゃなく、ワープロ (死語) で作ってますから…。
ネットになんか、つながってませんから…。
記録媒体、フロッピーディスク (死語) ですから…。
感熱紙 (死語) に印刷して、それをスマホで写真に撮って、画像をメールに添付しただけですから…。

若い先生方はたぶん『ワープロ (ワードプロセッサ) 』なんて機械、ご存知無いでしょうね。昭和末期〜平成初期の “遺物” のことですよ。

３ダースはパソコンは持ってませんし、有ったとしても使えません。
文書や表などは…いまだに、すべてワープロで作っております。

そんなショボめの資料ですが、もしご興味のある方には３ダース自作の木枠寸法表をコピーして差し上げますので、メールください。
郵送するか、納品の際にお持ちします。
※このサイトは３ダースさんのメルマガなので資料をご覧になることができます。

ひとくちに “Ｆ型” と言っても、木枠寸法のタテヨコの比率はまちまちです。

Ｆ４はけっこう細長くて、Ｆ８やＦ10は正方形に近い感じです。
コレ、意識したことありましたか？
もちろん油絵を専門でやって来た先生方にとっては “当然の常識” ですよね？

“細長いグループ” に属するのはＳＭ・Ｆ４・Ｆ60・Ｆ120。(ＳＭをＦ型とするか…には異論があるかもしれませんが…)
なお、大サイズのＦ200・Ｆ300・Ｆ500も…このグループです。

一方の… “正方形に近いグループ” に属するのはＦ８・Ｆ10・Ｆ20・Ｆ130です。

もうね、全っ然違いますよ、比率が…。

紙って一緒じゃないですか…？
Ａ４もＡ３も、Ｂ５もＢ４も…。
短辺１に対して長辺は1.414 (ルート２) 。

試しに大きさの違うコピー用紙を何種類か重ねてみてください。一つの角をピッタリ合うように重ねて…、対角線を結んでいくと一本の直線になりますよ。

木枠寸法ではそうは行きません。

細長いグループは…短辺１に対して長辺は1.3以上の細長さ！

正方形に近いグループは…短辺１に対して長辺は1.2以下です！
“１に対して1.2以下” ですよ！
特に『Ｆ10』なんかは…短辺１に対して長辺がたったの1.165程度です！
Ｆ10は…他の号数のＦ型と比べてみても、もう見るからに『別な形』です！　『異形』です！

同じ『Ｆ型』を名乗っているのに、なんで号数によって比率がまちまちなのでしょうか？

不思議ですよねぇ？
なんでだか…わかりますか？

 

それは『昔のヒトが適当にタテヨコの寸法を決めちゃったから』…です ‼

『木枠寸法全体を通しての “一律に決められた比率” なんて存在しないから』…です ‼

はい…みなさん、悩まないでください。
そんなモンです。
そんなモンなんです。

『木枠寸法のタテヨコ比率って、一律じゃないんだ。けっこういい加減に決められちゃったんだ』…と覚えていただいてオッケーです。

そう、適当なんですよ。木枠寸法なんて…。
崇高な、理想的な比率なんて有りません。マジで適当に作られていたんです。
そんなモンなんですよ。
生徒さんにもそうご説明なさってください。

そんな訳ですので、同じＦ型を名乗っていても…号数が変われば比率も変わっちゃうんです。
だって、１対1.489くらいの超〜細長いのから、１対1.165くらいの…ほぼ正方形みたいなのまでが、みんな “Ｆ型” を名乗っているんですから！
『Ｆ型の比率』を規定する厳密な基準なんて存在しないんです！
昔のヒトのやりたい放題で…こうなっちゃったんです。
こんな適当なことが “当たり前” なんですよ、油絵の世界では！

ですので、我々も “Ｆ型と言えども比率はまちまち” …という前提で物事を考えなければならないんですよ。

以前…『本番のキャンバスに油絵を描く前に、小振りな (紙製の) キャンバスボードに油絵具を使って下絵を描いてみましょう』…とご提案いたしましたが、本番のキャンバスの比率に合うようにキャンバスボードの方をカッターで切り…同じ比率に揃えてから下絵を描いていただきたいものです。

また、デスケル (デッサンスケール) にも “Ｆ型用” っていうのがありますが、使うキャンバスの比率と合っていなければまったく役に立ちません。かえって “害悪” です。
つまり、こんなモノを買っちゃうのはお金のムダなんですよ。
厚紙とカッターと糸とセロテープで、使うキャンバスの比率に合わせて…その都度自作するようにしましょうよ。

『え～？　木枠寸法ってそんなにいい加減なんですかぁ？　でもたぶん…３ダースｻﾝが知らないだけで、本当はなにかしらの基準が有るんじゃないですか？』って思うでしょ？
思いたくなるでしょ？

残念！
無いんですよ〜。

何らかの基準が有ったのなら、『１対1.489』も『１対1.165』も同じＦ型になるわけないですよね？
つまり、“統一基準” なんて有り得ません。
有りっこ無いでしょ？

でも、まぁ実は…画材業界内の通説では “それなりの基準” は有るってことになってます。
３ダースもその “通説” を信じ込んでましたよ、10年くらい前までは…。

もちろん今ではその『基準が有る…という説』は信じてません！
だって、昔のヒト達はそうした基準に従おうとしてた雰囲気なんかサラサラ無く…製造上の効率の方をはるかに優先しちゃってたみたいなんですもん。
そして、ついつい効率のみを追い求めたために…理想のカタチからもどんどんズレて行っちゃったんですよ。
最初から “基準” とか “理想のカタチ” とかが存在していたのかが、ホントに疑わしいくらいに…。

 

では一応…業界内で “通説” と言われている基準のことを、ちょっとご紹介しますわ。

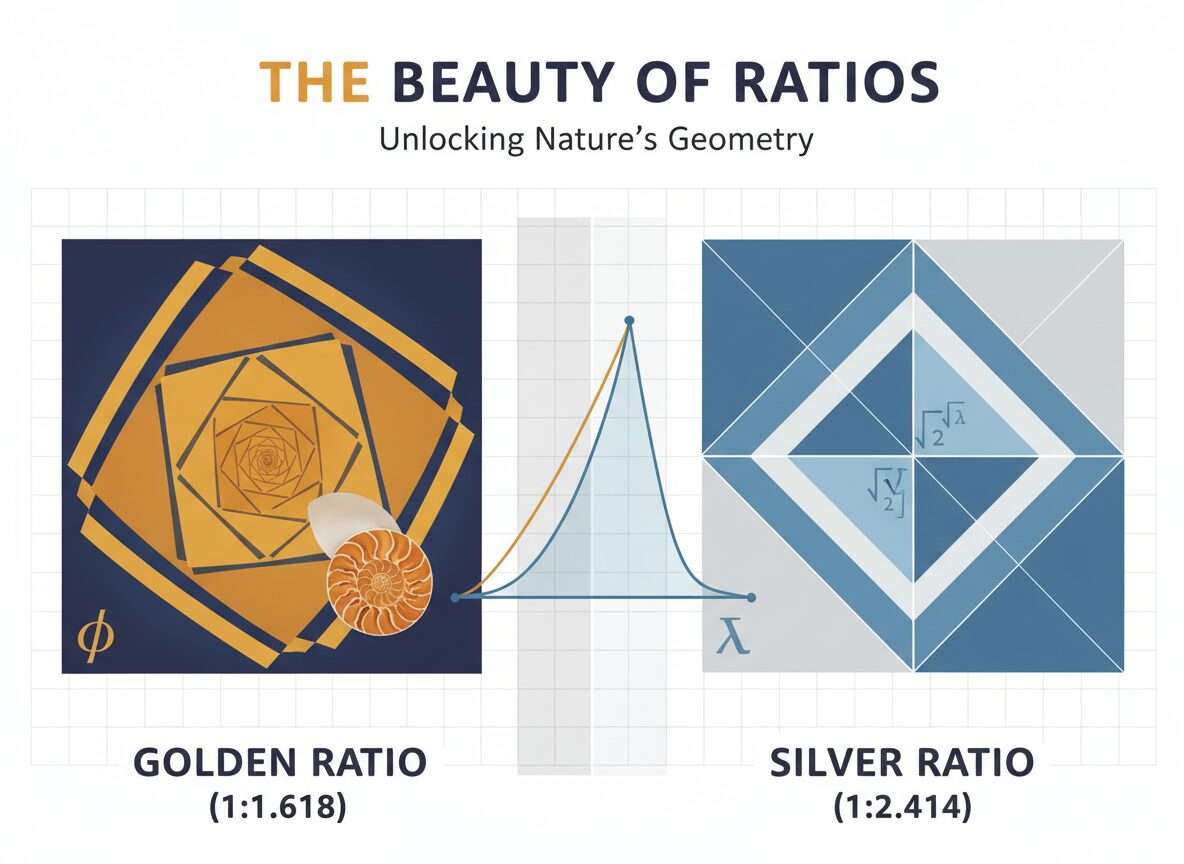
『１対1.618』
これ…みなさんご存知ですよね？
そう、『黄金比』ってヤツです。
西洋のヒト達がやたらと大好きな比率です。
日本ではそれほど優勢なカタチではありませんが、名刺の長方形がだいたいこの比率に近いらしいです。

Ｍ型キャンバスは、この黄金比 (短辺１に対して長辺が1.618) になるように設計されている…と、まことしやかに言われています。

そしてこのＭ型を、長辺の中央同士を結ぶ線で真っぷたつに切ると…二つのＦ型が出現します。
この、出現したＦ型の比率は短辺１に対して長辺1.236。

つまり “通説” によると、ＦとＭはどちらも黄金比をもとに作られていた…ってことになってるんですね。

Ｐ型は『白銀比』。すなわち紙の規格寸法の比率と同じで…短辺１に対して長辺が1.414になっている…と、まことしやかに言われています。

以上が、Ｆ・Ｐ・Ｍのタテマエとされる “通説” です。結構大勢の画材業界人がこの説を信じているはずです。

でもこれらは明らかに “後付けの理論” なんじゃないか？…と、３ダースは考えています。
つまりタテマエというような… “事前に存在したルール” みたいなモノではなく、後の世代の…ちょっと頭の良いヒトが注目を浴びようとして創作した “後付けストーリー” なのでしょう。

３ダースは通説否定派です !!!!

業界内の先輩達は…かしこぶって黄金比とか白銀比とか言っちゃってるけど、この説は絶対にウソですよ！
完全なデマなんですよ！
３ダースはそう思うんですよ！

なぜ３ダースは画材業界全体を敵に回すような強硬な言い方が出来るのか？…というと、それは木枠寸法表を見ながら全サイズの比率の計算をしてみたから。

 

計算して出て来た答えを見て、通説を鵜呑みしちゃダメだ…って気付いたから。　

だって、この通説通りの比率で作られてる木枠は…確かに有るには有るんですけど、マジで…、マジで少数派だったんですよ。
ちょっと計算してみれば『通説なんて絶対ウソだ』って…誰でも確信できます。

何度でも繰り返しますが、この “通説” は『ガセ』(真偽不明な情報) とも言えそうですが、実際はもっと悪質な『デマ』(悪意の有る…意図的なウソ情報) なのです！

計算すれば計算するほど、通説のウソが浮かび上がって来ますよ。
まぁ３ダースが徹底的に計算しておきましたから、みなさんはイチイチ計算しなくて大丈夫ですからね。

では実証してみましょう！

 ※ なお、１号・２号・５号は実質存在しない寸法なので、ここでは無視します。

通説によると、Ｆ型の理想の比率は短辺１に対して長辺が1.236でしたよね？
この理想の比率にほぼ近いのは…
Ｆ３ (１対1.241)
Ｆ15 (１対1.230)
Ｆ25 (１対1.232)
Ｆ40 (１対1.245)
Ｆ100 (１対1.243)
と、全体の中でたったの５つのみ。
(短辺を１として…長辺が1.226〜1.246の範囲でピックアップ)

逆に、他の大多数のＦ型は理想のカタチからはハズレている…と言うことが出来ます。

今回の冒頭でも述べましたが、細長いグループなんかは…
ＳＭ (１対1.437)
Ｆ４ (１対1.376)
Ｆ60 (１対1.343)
Ｆ120 (１対1.489)
Ｆ200 (１対1.335)
Ｆ300 (１対1.334)
Ｆ500 (１対1.341)
と、こんな感じです。

正方形に近いグループは…
Ｆ８ (１対1.197)
Ｆ10 (１対1.165)
Ｆ20 (１対1.200)
Ｆ130 (１対1.198)
と、こんな感じ。

もうこれで、Ｆ型は黄金比に由来するっていう “後付けの理想論” は破綻していることがわかりますよね 

 

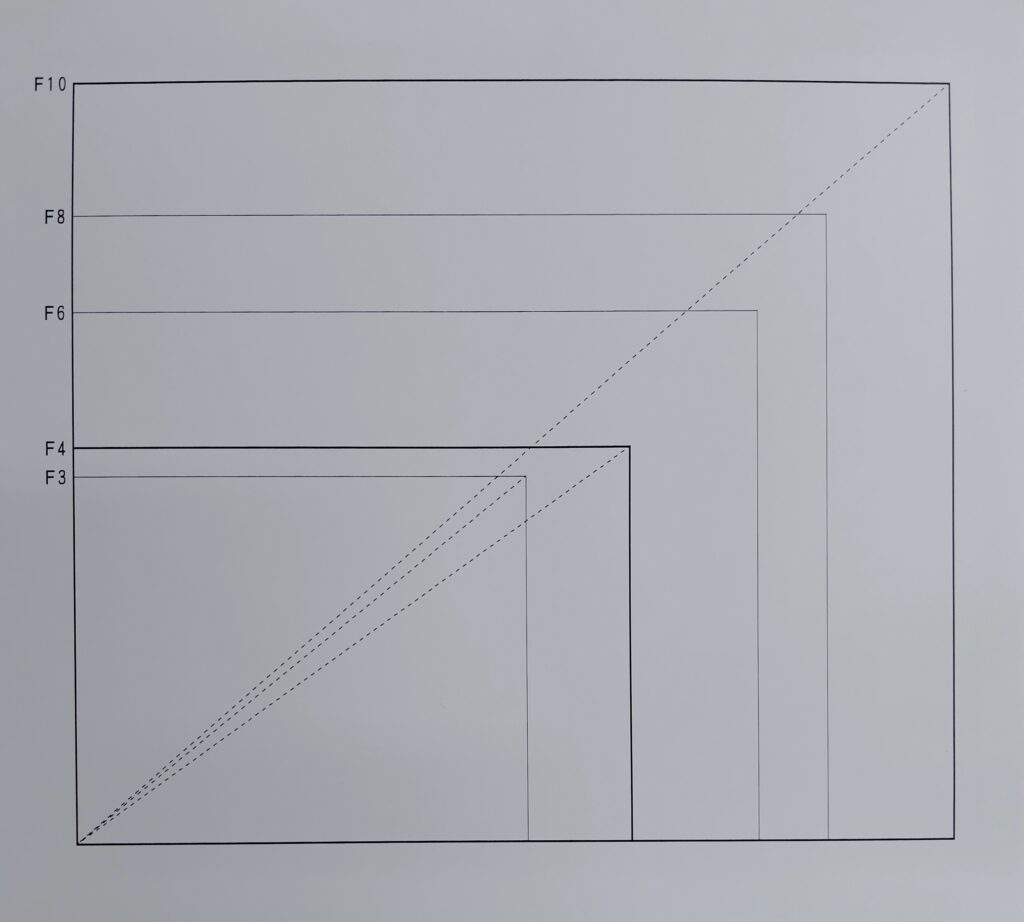
※添付画像

※添付画像をご覧ください。
通説で言う “理想のＦ型” に近い『Ｆ３』と、細長グループの『Ｆ４』…正方形に近いグループの『Ｆ10』に対角線を付けてみました。
カタチの違い、一目瞭然でしょ？

Ｐなんか、もっとひどいんですよ。
理想のＰ型 (短辺１に対して長辺が1.414) の比率に “近い” と言えるのは、全体の中で
Ｐ200 (１対1.425)
の…たった１つだけしか有りません！
(短辺を１として…長辺が1.404〜1.424の範囲でピックアップするつもりでしたが、唯一これに近かったこのＰ200でさえ…四捨五入したらその “範囲” からはみ出しました)

しかも中には…Ｐのくせに短辺１に対して長辺1.5以上の “細長過ぎるヤツ” までありますからね。
Ｐ６ (１対1.502)
Ｐ80 (１対1.5)
Ｐ120 (１対1.732)
Ｐ500 (１対1.527) などが、それ。

ね？　白銀比に近い “理想の比率” は全体の中でたったの１つしか無かったのに、１対1.5以上の細長過ぎる比率のは４つも有るんですよ。
“Ｐは白銀比で出来ている” なんて、完全にデマ (ウソ) ですわ。

Ｍは…
Ｍ60 (１対1.623) と
Ｍ80 (１対1.628) が理想的な黄金比と言えるでしょう。
(短辺を１として…長辺が1.608〜1.628の範囲でピックアップ)

この二つはほぼ完璧な黄金比です！
素晴らしい！
でも…理想の比率の範囲に収まるのは全体の中でこの２つだけ。

それにＭ15 (１対1.433) や
Ｍ20 (１対1.454) はＰ並みの比率です。
結局、“Ｍは黄金比の長方形になるように設計されている” っていうのもデマ (ウソ) だったんですわ。

いかがですか？
３ダースの言う通り…もともとタテマエ的な基準なんてものは無かったんですよ。
最初に木枠を作ったヒトが、勝手な寸法で作っちゃっただけのこと。
皆さんが思ってるより、はるかに適当に作られていたんです。

ガッカリしないでくださいね。木枠なんて…そんなモンです。そんなモンなんです。

最後に、一つだけ面白いサイズがありましたのでご紹介しましょう。
『Ｍ60』です。

ついさっき…このＭ60は『理想的な黄金比だ』と申しましたが、これの長辺の中央同士を結ぶ線で半分に切断すると…見事に２枚のＦ25が出現するんです。 (厳密に言うと0.5㎜足りないんですけど )

こういう関係性が全体の中でたった１つの例だけでなく…他にもたくさんあったのなら、通説の正しさを証明できたのでしょうが、たったの１件だけなんですよ。

すべてのＭ型を真っぷたつに切ると小さい２枚のＦ型が出現する…って言うんならマジで面白いんですけどね。

全然そうなっていないんだから『崇高な、理想的な比率』なんか最初っから無く、“適当に寸法を決めて作っていた” …と考えるべき。

黄金比だの白銀比だのに従って木枠のカタチが設計された…っていう理想論は、完全な後付けなんです。
しかもそれはデマ…すなわち悪意を感じられるくらいのウソ情報だったのです。

【第47回終わり】